ニュース 正ハ面体とは何ですか？. トピックに関する記事 – 正多面体にはどんな性質がありますか？

つまり、正多面体は「どの面もすべて合同な正多角形」という性質があります。 さらにもうひとつ、「どの頂点にも面が同じ数だけ集まっている」という性質もあります。 正八面体はどの頂点にも４面が集まっているので正多面体です。正八面体は3方向軸で直交していて、三角錐を合わせた双角錐である。 正八面体はまた、4方向軸で反角柱である。 八面体は3次元の正軸体である。八つの平面で囲まれる立体。

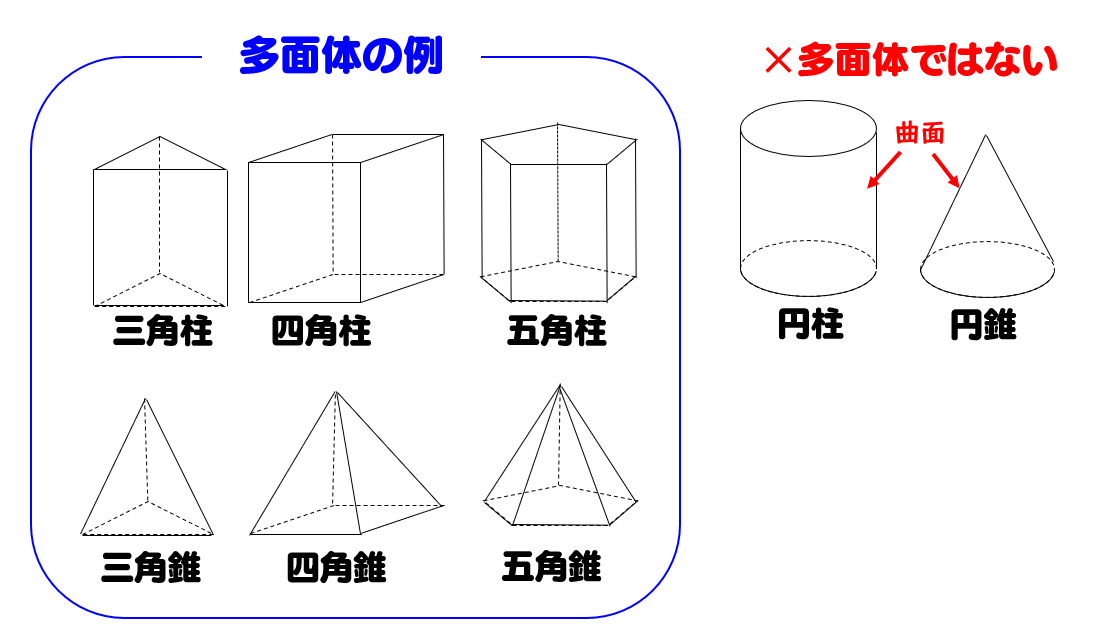
正多面体の辺の数の計算方法は？正多面体の辺の数 多面体では，どの辺も隣り合う２つの面（多角形）の辺になっているので，正多面体では，(辺の数)＝(１つの面の辺の数)×(面の数)÷２の関係が成り立つ。

正多面体はなぜ5つしかないのですか？

１つの頂点に正五角形が３枚ずつ集まると正十二面体ができますが、正五角形の１つの内角は１０８度なので、正五角形４枚の角度の和は360度以上となり、これ以上の枚数の正五角形で正多面体を作ることはできません。 これが、正多面体が５種類しかない理由です。高校1年生の数学A「空間図形と多面体」の単元となるので、先取り学習となります。 正多面体には、正四面体・正六面体・正八面体・正十二面体・正二十面体の5種類があります。

正八面体の1つの頂点に集まる面はいくつですか？

【コラム第4回】正多角形と正多面体の話

	面の形	１頂点を共有する面
正六面体	正四角形	3
正八面体	正三角形	４
正十二面体	正五角形	3
正二十面体	正三角形	5

このことを使って、例えば正八面体の頂点の数を求めてみましょう。 正八面体は頂点に4つの面が集まるので、3×8÷4=6個です。

正何面体の辺の数は？

【結構ムズイ】多面体の辺や頂点の数

	面の数	辺の数
正四面体	４	６
正六面体	6	12
正八面体	8	12
正十二面体	12	30

【考え方】 正二十面体ですから，面の数は２０です。「1つの面の辺の数×面の数÷２」

例えば正八面体は正三角形が８個集まっています。 正三角形には３本の辺があるので、バラバラ状態では合計で3×8=24本の辺があります。

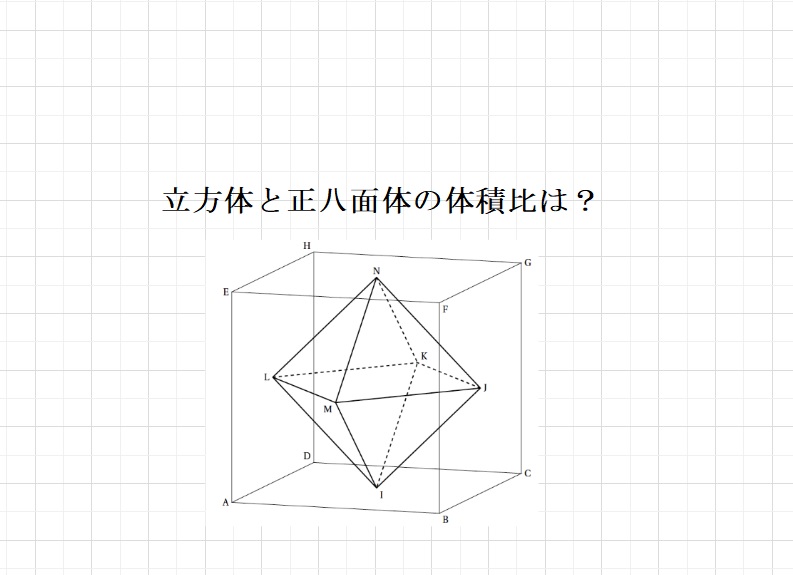
（２）１つの頂点に集まる辺の数と面の数がどこも同じとなります。 全部で５つ、正四面体、正六面体、正八面体、正十二面体、正二十面体が正多面体です。

正多面体は本当に5種類あるか？正多面体は、正四面体、正六面体、正八面体、正十二面体、正二十面体の5種類しか存在しない!

正多面体が存在する条件は？正多面体とは・・・ ① どの面も合同な正多角形になっている。 ② どの頂点にも同じ数の面が集まっている。 ①②の性質をもち， へこみのないものが正多面体です。

正八面体の辺の数はどうやって求めるの？

「1つの面の辺の数×面の数÷２」

例えば正八面体は正三角形が８個集まっています。 正三角形には３本の辺があるので、バラバラ状態では合計で3×8=24本の辺があります。 これを貼り合わせると、2本の辺がそれぞれ1組になって1本になります。 よって、正八面体の辺は24÷2=12本となります。

また逆に, 正八面体の8つの面の中心に点をとり、そ の点を結んでいくと、正六面体 (立方体)が生まれる(図9)。 さらに,正十二面体と正二十面体の間に も同じような関係がある。１つの頂点に正五角形が３枚ずつ集まると正十二面体ができますが、正五角形の１つの内角は１０８度なので、正五角形４枚の角度の和は360度以上となり、これ以上の枚数の正五角形で正多面体を作ることはできません。 これが、正多面体が５種類しかない理由です。正二十面体の２０個の面をすべてバラバラにすると正三角形が２０枚。