ニュース 比の値 なんのため？. トピックに関する記事 – なぜ比を使うのか？

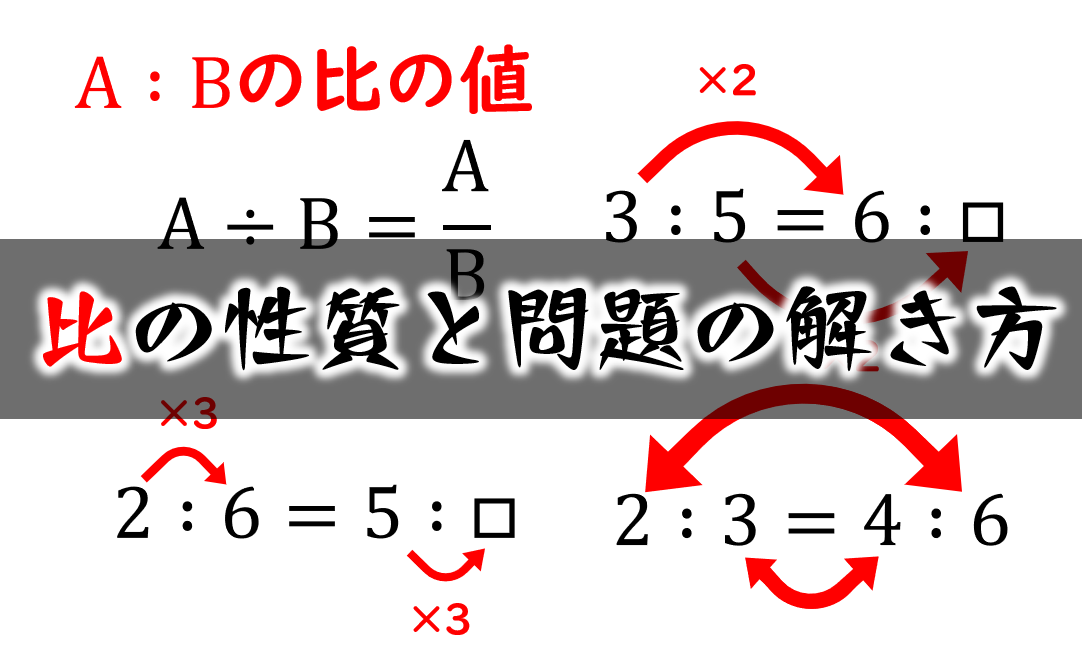
“比”とは、２つの量の割合を「：」の記号を使って表したものをいいます。 比を使うと、分数や少数を使わずにかんたんな整数だけで２つの量の割合をすっきりと表すことができます。 今までに学習した約分や最小公倍数、分数などが多く出てくるので、復習してみるといいでしょう。a：bの比の値は，a÷bで求められます。 a：bの比の値は，aがbの何倍になっているかを表す数です。「比は，日常生活のいろいろな場面で用いられる。 例 えば，二つの液量を混合したり，二つの長さを組み合わ せたりするなど，部分と部分どうしを考察する場面，二 つの数量を配分する場面で，数量の関係を比で表現し， 等しい比をつくるなどして考察した結果を活用して，課 題を解決する。

比とその利用とはどういうことでしょうか？２つの数量の割合を簡単に表せる比のよさに気付き、それを用いようとする。 割合と比を関連付けてとらえ、考えたことを筋道を立てて表現し、比を用いて考えている。 ２つの数量の割合を比を用いて表したり、等しい比を見つけたり、比を簡単にしたりすることができる。

比の値が等しいことを何といいますか？

６：８と９：12のように、２つの比の値が等しいとき、割合も等しくなっています。 このことを、｢２つの比は等しい」と言い、６：８＝９：12と書きます。比は小学校6年生の算数で習う単元だが、こうした基礎の基礎を意外に理解していないことがある。 たとえば「4」と「5」という数字がある。 その割合は「4：5」と表す。

比例の値を求めるには？

比例の a は「 a = y÷x 」で求める！ （ⅱ）反比例の式は必ず「 y = a/x 」（ こちらも a のことを『比例定数』という）のかたち！

比は小学校6年生の算数で習う単元だが、こうした基礎の基礎を意外に理解していないことがある。 たとえば「4」と「5」という数字がある。 その割合は「4：5」と表す。

比の値が等しいとはどういうことか？

二つの比の値が等しいとき、二つの比は等しいといいます。 Ａ：Ｂの両方の数に同じ数をかけたり、両方の数を同じ数でわったりしてできる比は、みんなＡ：Ｂに等しくなります。このように比の値が等しいとき、それらの「比は等しい」（等しい比）という。 そして「4：5＝8：10」と表すことができる。「３組の辺の比がすべて等しい」 ならば、２つの三角形は相似だといえるんだ。

たいてい高校２年生※の 『 数Ｂ 』 の授業で、『 ベクトル 』 という単元の学習をします。 【 ※中高一貫校や進学校の一部では、もっと早い時期に学習する場合があります。 】

比例式のルールは？比例式には、「内項（BとC）の積と外項（AとD）の積は等しい」という性質がある。 つまり、「A：B＝C：Dのとき、B×C＝A×D」という公式が成り立つ。 実例として「5：4＝10：8」で確かめてみると、「内項の積は4×10＝40、外項の積は5×8＝40」で確かに等しい。

中学で習う比例とは？「比例」とは、前回学習した「関数」の一種だよ。 関数の式の中でも、 「ｙ＝□ｘ」の形で表せる特別な式 のとき、 「ｙがｘに比例する」 というんだよ。 「ｙ＝□ｘ」の□に入るのは、２や３などの具体的な数字なんだ。 に入る具体的な数字 のことは、 「比例定数」 と呼んでいるよ。

6年生で習う算数一覧は？

単元確認問題小学校６年生算数

• 対称な図形
• 文字と式
• 分数と整数のかけ算・わり算
• 分数のかけ算
• 分数のわり算
• 比

サイン・コサインを習うのは高校の数IA。 小学生がそれを知っているのは優秀ですが，しかし，この発言には，「サイン・コサインを習って何の役に立つの・・・」といったニュアンスも含まれる気がします。 サイン・コサインは，もちろん，とても重要な関数です。45（5分の4、ごぶんのよん）は、有理数のうち 0 と 1 の間にある数であり、 15 の4倍である。 十進法で小数表示すると、0.8 である。3つの辺の比が3：4：5になっていれば、必ず直角三角形になります。 諸説ありますが、古代エジプトではこの形を使って直角を計り、ピラミッドを作ったのではないか、と言われているように昔から知られている形です。 整数だけで三平方の定理が成立する三辺の比のグループのことを、‟ピタゴラス数“といいます。